As we discussed how OLS works, we turn to another popular regression method often used in Machine Learning algorithms – Ridge. In the article, we are going to discuss what Ridge regression is, how it is different from OLS, why we need this difference, and how we can calculate the Ridge estimator.
Intro
In OLS, we aim to minimize the sum of the squared differences between the predicted values and the actual values of the dependent variable, as shown by the following equation:
![]()
where ![]() is the vector of observed values,
is the vector of observed values, ![]() is the matrix of predictors, and
is the matrix of predictors, and ![]() is the vector of coefficients that we want to estimate. However, when the number of predictors is large, OLS can lead to overfitting, which means that the model is too complex and doesn’t generalize well to new data.
is the vector of coefficients that we want to estimate. However, when the number of predictors is large, OLS can lead to overfitting, which means that the model is too complex and doesn’t generalize well to new data.
To address this issue, Ridge Regression adds a penalty term to the OLS loss function, which aims to shrink the coefficients towards zero. This penalty term is controlled by a hyperparameter ![]() , which can be tuned to find the optimal balance between model complexity and performance. The Ridge Regression objective function can be written as:
, which can be tuned to find the optimal balance between model complexity and performance. The Ridge Regression objective function can be written as:
![]()
where ![]() denotes the squared Euclidean norm. By adding the penalty term, Ridge Regression is able to reduce the size of the coefficients and avoid overfitting, while still maintaining good performance on the training data.
denotes the squared Euclidean norm. By adding the penalty term, Ridge Regression is able to reduce the size of the coefficients and avoid overfitting, while still maintaining good performance on the training data.
Ridge Estimators
To calculate the Ridge estimators, we need to solve the following optimization problem:
![Rendered by QuickLaTeX.com \[\hat{\beta}_{Ridge} = arg \min_{\beta} \{ (\mathbf{y} - \mathbf{X}\boldsymbol{\beta})^\top (\mathbf{y} - \mathbf{X}\boldsymbol{\beta}) + \lambda \sum_{j=1}^{p} \beta_j^2 \}\]](https://zhangyuantong.com/wp-content/ql-cache/quicklatex.com-04993cdc1e882df08390dfdb7a009328_l3.png)
where ![]() is the
is the ![]() matrix of predictors,
matrix of predictors, ![]() is the
is the ![]() vector of response variables,
vector of response variables, ![]() is the
is the ![]() vector of coefficients to be estimated, and
vector of coefficients to be estimated, and ![]() is the penalty parameter that controls the amount of shrinkage applied to the coefficients.
is the penalty parameter that controls the amount of shrinkage applied to the coefficients.
Using the matrix notation, we can write the objective function as:
![]()
To find the Ridge estimators, we need to take the derivative of the objective function with respect to the coefficient vector ![]() and set it equal to zero:
and set it equal to zero:
![]()
Solving for ![]() , we get:
, we get:
![]()
where ![]() is the
is the ![]() identity matrix. This expression shows that the Ridge coefficients are obtained by multiplying the inverse of the sum of the squared predictors and the penalty parameter by the matrix product of the transpose of the predictors and the response variables.
identity matrix. This expression shows that the Ridge coefficients are obtained by multiplying the inverse of the sum of the squared predictors and the penalty parameter by the matrix product of the transpose of the predictors and the response variables.
It is important to note that the matrix ![]() is always invertible, which ensures that the Ridge estimators exist and are unique. Moreover, the Ridge estimators can be computed efficiently using standard matrix inversion algorithms, such as the QR decomposition or the Singular Value Decomposition (SVD).
is always invertible, which ensures that the Ridge estimators exist and are unique. Moreover, the Ridge estimators can be computed efficiently using standard matrix inversion algorithms, such as the QR decomposition or the Singular Value Decomposition (SVD).
Reduce Sizes and Avoid Overfitting
To see why this shrinks the size of estimators and avoids overfitting, let’s focus on the expression of the Ridge estimator:
![]()
The expression ![]() is known as the Ridge Regression shrinkage operator. It can be shown that the coefficients estimated by Ridge Regression are proportional to the coefficients estimated by OLS, but scaled down by a factor that depends on the value of
is known as the Ridge Regression shrinkage operator. It can be shown that the coefficients estimated by Ridge Regression are proportional to the coefficients estimated by OLS, but scaled down by a factor that depends on the value of ![]() . Specifically, the Ridge coefficients are given by:
. Specifically, the Ridge coefficients are given by:
![]()
where ![]() is the OLS estimate for the
is the OLS estimate for the ![]() -th coefficient, and
-th coefficient, and ![]() is a scaling factor that depends on the data. As we can see from this expression, the Ridge coefficients are always smaller than the OLS coefficients, since the denominator is always greater than 1.
is a scaling factor that depends on the data. As we can see from this expression, the Ridge coefficients are always smaller than the OLS coefficients, since the denominator is always greater than 1.
To see how this helps to avoid overfitting, consider the case where the number of predictors is large relative to the number of observations in the training data. In this scenario, OLS may produce a model with coefficients that have large absolute values, resulting in a complex model that is susceptible to overfitting. Ridge Regression, on the other hand, will produce a model with smaller coefficient values, because of the penalty term. This reduction in the size of the coefficients reduces the complexity of the model and makes it less likely to overfit.
![]()
This expression shows that the coefficients in Ridge Regression are a function of both the original OLS coefficients, ![]() , and the penalty term,
, and the penalty term, ![]() . The penalty term shrinks the coefficients towards zero, and the amount of shrinkage is controlled by the value of
. The penalty term shrinks the coefficients towards zero, and the amount of shrinkage is controlled by the value of ![]() . As
. As ![]() increases, the size of the coefficients decreases, and the model becomes simpler.
increases, the size of the coefficients decreases, and the model becomes simpler.
Intuitively, the Ridge penalty term shrinks the coefficients towards zero by imposing a trade-off between the goodness of fit and the complexity of the model and helps to avoid overfitting by adding a penalty term to the OLS loss function, which encourages the coefficients to have smaller absolute values. When the penalty parameter ![]() is large, the Ridge coefficients will be close to zero, which means that the model is simpler and less prone to overfitting. On the other hand, when
is large, the Ridge coefficients will be close to zero, which means that the model is simpler and less prone to overfitting. On the other hand, when ![]() is small, the Ridge coefficients will be closer to the OLS estimates, which means that the model is more complex and can fit the data more closely, but may be more prone to overfitting.
is small, the Ridge coefficients will be closer to the OLS estimates, which means that the model is more complex and can fit the data more closely, but may be more prone to overfitting.
Biasedness and Consistency
The Ridge estimator is biased.
This is because the addition of the penalty term in Ridge Regression results in a bias in the estimated coefficients, compared to the OLS estimates.
To see this, consider the expected value of the Ridge estimator:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{aligned} \mathbb{E}(\boldsymbol{\beta}^{\text{Ridge}}) &= \mathbb{E}\left[(\mathbf{X}^\top\mathbf{X} + \lambda \mathbf{I})^{-1}\mathbf{X}^\top\mathbf{y}\right]\ \\ &= \mathbb{E}\left[(\mathbf{X}^\top\mathbf{X} + \lambda \mathbf{I})^{-1}\mathbf{X}^\top(\mathbf{X}\boldsymbol{\beta}+\boldsymbol{\epsilon})\right]\ \\ &= \mathbb{E}\left[(\mathbf{X}^\top\mathbf{X} + \lambda \mathbf{I})^{-1}\mathbf{X}^\top\mathbf{X}\boldsymbol{\beta}\right] + \mathbb{E}\left[(\mathbf{X}^\top\mathbf{X} + \lambda \mathbf{I})^{-1}\mathbf{X}^\top\boldsymbol{\epsilon}\right] \end{aligned} \end{equation*}](https://zhangyuantong.com/wp-content/ql-cache/quicklatex.com-d3f1319b548137e124fe375143541e48_l3.png)
where ![]() is the error term, assumed to have mean zero and constant variance.
is the error term, assumed to have mean zero and constant variance.
The first term on the right-hand side of the equation is the bias term, which can be shown to be:
![]()
The second term on the right-hand side of the equation is the variance term, which has mean zero and can be shown to be:
![Rendered by QuickLaTeX.com \begin{equation*} \begin{aligned} \mathbb{E}\left[(\mathbf{X}^\top\mathbf{X} + \lambda \mathbf{I})^{-1}\mathbf{X}^\top\boldsymbol{\epsilon}\right] &= (\mathbf{X}^\top\mathbf{X} + \lambda \mathbf{I})^{-1}\mathbf{X}^\top\mathbb{E}(\boldsymbol{\epsilon})\ \\ &= (\mathbf{X}^\top\mathbf{X} + \lambda \mathbf{I})^{-1}\mathbf{X}^\top\mathbf{0}\ \\ &= \mathbf{0} \end{aligned} \end{equation*}](https://zhangyuantong.com/wp-content/ql-cache/quicklatex.com-dec782ba6515ce8c8360a436afc73530_l3.png)
Therefore, the expected value of the Ridge estimator is:
![]()
which is a biased estimator of the true regression coefficients ![]() . The bias is a function of the tuning parameter
. The bias is a function of the tuning parameter ![]() and the true regression coefficients
and the true regression coefficients ![]() .
.
However, even though the Ridge estimator is biased, it can still lead to better prediction performance by reducing the variance of the estimates, as explained earlier. The amount of bias introduced by Ridge Regression is typically small compared to the reduction in variance, especially when the number of predictors is large relative to the sample size.
The Ridge estimator is consistent.
In statistics, consistency means that as the sample size ![]() approaches infinity, the estimator converges in probability to the true value of the parameter being estimated.
approaches infinity, the estimator converges in probability to the true value of the parameter being estimated.
For Ridge Regression, the estimator is consistent because the penalty term added to the least squares objective function ensures that the estimated coefficients do not grow unbounded even when the number of predictors is larger than the sample size.
The consistency of the Ridge estimator can be shown mathematically by demonstrating that as the sample size ![]() approaches infinity, the estimated coefficients converge in probability to the true regression coefficients. Specifically, under some regularity conditions, it can be shown that:
approaches infinity, the estimated coefficients converge in probability to the true regression coefficients. Specifically, under some regularity conditions, it can be shown that:
![]()
for any positive value of ![]() , where
, where ![]() is the Ridge estimator and
is the Ridge estimator and ![]() is the true regression coefficients.
is the true regression coefficients.
Showing the consistency of Ridge Regression involves demonstrating that as the sample size ![]() approaches infinity, the Ridge estimator
approaches infinity, the Ridge estimator ![]() converges in probability to the true regression coefficients
converges in probability to the true regression coefficients ![]() .
.
Specifically, we need to show that:
![]()
for any positive value of ![]() .
.
To prove this, we first define the Ridge estimator as:
![]()
where ![]() is the
is the ![]() design matrix,
design matrix, ![]() is the
is the ![]() response vector,
response vector, ![]() is the tuning parameter, and
is the tuning parameter, and ![]() is the
is the ![]() identity matrix.
identity matrix.
Next, we express the difference between the Ridge estimator and the true coefficients as:
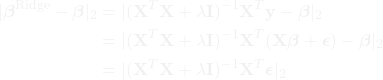
where ![]() is the
is the ![]() vector of errors.
vector of errors.
Using the triangle inequality, we have:
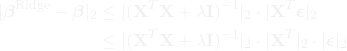
where we have used the sub-multiplicative property of matrix norms and the fact that ![]() .
.
Now, to show that the Ridge estimator is consistent, we need to show that both terms on the right-hand side of the above inequality converge to zero as ![]() .
.
First, note that by the strong law of large numbers, we have ![]() as
as ![]() , where
, where ![]() is the
is the ![]() covariance matrix of the predictor variables. Since
covariance matrix of the predictor variables. Since ![]() , it follows that
, it follows that ![]() almost surely.
almost surely.
Next, note that by the Cauchy-Schwarz inequality, we have:
![]()
Since ![]() almost surely and
almost surely and ![]() , it follows that
, it follows that ![]() almost surely.
almost surely.
Finally, we note that ![]() is a continuous function of
is a continuous function of ![]() , and hence is bounded over any finite interval of
, and hence is bounded over any finite interval of ![]() . This means that there exists some constant
. This means that there exists some constant ![]() such that
such that ![]() for all
for all ![]() and all
and all ![]() .
.
Putting everything together, we have:
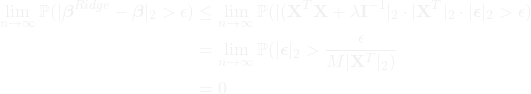
where the last step follows from the fact that ![]() almost surely.
almost surely.
Therefore, we have shown that the Ridge estimator is consistent, which means that as the sample size ![]() gets larger and larger, the estimator will converge to the true coefficients with high probability.
gets larger and larger, the estimator will converge to the true coefficients with high probability.