Table of Contents
Introduction to Linear Regression
Linear regression is a statistical method used to model the relationship between a dependent variable and one or more independent variables. In its simplest form, linear regression assumes a linear relationship between the dependent variable ![]() and one independent variable
and one independent variable ![]() :
:
![]()
where ![]() is the intercept,
is the intercept, ![]() is the slope coefficient, and
is the slope coefficient, and ![]() is the error term. The goal of linear regression is to estimate the values of the parameters
is the error term. The goal of linear regression is to estimate the values of the parameters ![]() and
and ![]() that best fit the data.
that best fit the data.
Assumptions of Linear Regression
Before estimating the parameters of a linear regression model, we need to check that the following assumptions are satisfied:
- Linearity: The relationship between the dependent variable
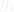 and the independent variables
and the independent variables 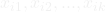 is linear in the parameters
is linear in the parameters 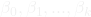 , i.e.,
, i.e.,
![]()
- Independence: The errors
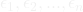 are independent and identically distributed (i.i.d.). This means that the probability distribution of each error is the same and that the occurrence of one error does not affect the occurrence of another error.
are independent and identically distributed (i.i.d.). This means that the probability distribution of each error is the same and that the occurrence of one error does not affect the occurrence of another error. - Homoscedasticity: The errors
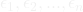 have the same variance
have the same variance  , i.e.,
, i.e.,  for all
for all  .
. - No Autocorrelation: There is no correlation between the errors at different observation points, i.e.,
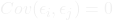 for all
for all  .
. - Exogeneity: The regressors
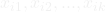 are uncorrelated with the errors
are uncorrelated with the errors  , i.e.,
, i.e., 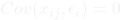 for all
for all  and
and 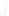 . This assumption is also known as the “no omitted variables” assumption.
. This assumption is also known as the “no omitted variables” assumption.
If these assumptions are not met, the results of the linear regression analysis may be biased or unreliable.
Ordinary Least Squares (OLS)
The most commonly used method to estimate the parameters of a linear regression model is Ordinary Least Squares (OLS). OLS estimates the parameters by minimizing the sum of squared errors:
![]()
where ![]() is the vector of OLS estimators,
is the vector of OLS estimators, ![]() is the vector of observed values of the dependent variable, and
is the vector of observed values of the dependent variable, and ![]() is the design matrix of the independent variables. The OLS estimators are given by:
is the design matrix of the independent variables. The OLS estimators are given by:
![]()
To show that the OLS estimators are unbiased and consistent, we need to make some assumptions. Under the assumptions of the Gauss-Markov theorem, the OLS estimators are unbiased:
![]()
where ![]() is the true vector of coefficients. The OLS estimators are also consistent:
is the true vector of coefficients. The OLS estimators are also consistent:
![]()
where ![]() is the sample size.
is the sample size.
Derivation of OLS Estimators
To derive the OLS estimators, we start by writing the sum of squared errors in matrix form:
![]()
Expanding and simplifying, we get:
![]()
To minimize this expression with respect to ![]() , we take the derivative with respect to
, we take the derivative with respect to ![]() and set it equal to zero:
and set it equal to zero:
![]()
Solving for ![]() , we get the OLS estimators:
, we get the OLS estimators:
![]()
Variance of OLS Estimators
The variance of the OLS estimators can be estimated using the formula:
![]()
where ![]() is the variance of the error term
is the variance of the error term ![]() .
.
Since ![]() is unknown, it is typically estimated using the residuals:
is unknown, it is typically estimated using the residuals:
![]()
where ![]() is the vector of residuals and
is the vector of residuals and ![]() is the number of regressors in the model (excluding the constant term).
is the number of regressors in the model (excluding the constant term).
Substituting ![]() for
for ![]() in the formula for the variance of the OLS estimators, we get:
in the formula for the variance of the OLS estimators, we get:
![]()
This expression gives an estimate of the variance-covariance matrix of the OLS estimators. Each diagonal element of this matrix represents the variance of the corresponding OLS estimator, while each off-diagonal element represents the covariance between two OLS estimators.
It is worth noting that this formula assumes that the error terms are homoscedastic (i.e., have equal variances) and that they are uncorrelated with each other and with the regressors. If these assumptions are violated, the formula for the variance-covariance matrix may need to be adjusted using techniques such as heteroscedasticity-robust standard errors or cluster-robust standard errors.
Derivation of Variance
To derive the variance of the OLS estimators, we need to start with the OLS estimator for ![]() , which we know is given by:
, which we know is given by:
![]()
where ![]() is the matrix of regressors,
is the matrix of regressors, ![]() is the vector of the dependent variable, and
is the vector of the dependent variable, and ![]() is the inverse of the matrix product
is the inverse of the matrix product ![]() .
.
Now, we want to find the variance of this estimator. The variance of the OLS estimator can be defined as:
![]()
where ![]() is the true population parameter vector. Expanding this expression, we get:
is the true population parameter vector. Expanding this expression, we get:
![]()
where ![]() is the vector of errors, i.e.,
is the vector of errors, i.e., ![]() .
.
Using matrix algebra, we can simplify this expression as follows:
![]()
where we have used the fact that ![]() and
and ![]() , where
, where ![]() is the identity matrix of size
is the identity matrix of size ![]() .
.
Therefore, the variance of the OLS estimators can be estimated as:
![]()
where ![]() is an estimate of the variance of the errors, calculated as:
is an estimate of the variance of the errors, calculated as:
![]()
where ![]() is the vector of residuals, and
is the vector of residuals, and ![]() is the number of regressors in the model (excluding the constant term).
is the number of regressors in the model (excluding the constant term).
Proof of Unbiasedness
To show that the OLS estimators are unbiased, we need to show that:
![]()
where ![]() is the true vector of coefficients.
is the true vector of coefficients.
We start with the OLS estimators:
![]()
Taking the expected value of both sides, we get:
![]()
Using the linearity of expectation, we can move the expectation inside:
![]()
Since ![]() is generated from the model
is generated from the model ![]() , we know that:
, we know that:
![]()
Substituting this into the previous equation, we get:
![]()
Therefore, the OLS estimators are unbiased.
Proof of Consistency
To show that the OLS estimators are consistent, we need to show that:
![]()
where ![]() is the sample size.
is the sample size.
We can rewrite the OLS estimators as:
![]()
Taking the norm of both sides, we get:
![]()
Using the Cauchy-Schwarz inequality, we can bound the norm of the OLS residuals:
![]()
Since ![]() is bounded and
is bounded and ![]() is finite, we only need to show that
is finite, we only need to show that ![]() goes to zero as
goes to zero as ![]() goes to infinity.
goes to infinity.
By the Law of Large Numbers, we know that:
![]()
where ![]() is a column vector of the independent variables. Under the assumption that
is a column vector of the independent variables. Under the assumption that ![]() is full rank, we can use the Central Limit Theorem to show that:
is full rank, we can use the Central Limit Theorem to show that:
![]()
where ![]() is the variance-covariance matrix of the independent variables. Since
is the variance-covariance matrix of the independent variables. Since ![]() is the inverse of
is the inverse of ![]() , we can write:
, we can write:
![]()
Using the matrix inversion lemma, we can rewrite this expression as:
![]()
Taking the norm of both sides, we get:
![]()
Since ![]() is full rank, we know that its inverse exists and is bounded. Therefore, we only need to show that
is full rank, we know that its inverse exists and is bounded. Therefore, we only need to show that ![]() goes to zero as
goes to zero as ![]() goes to infinity.
goes to infinity.
Using the same argument as before, we can show that:
![]()
By the Continuous Mapping Theorem, we have:
![]()
Therefore, we have shown that ![]() goes to zero as
goes to zero as ![]() goes to infinity, which implies that the OLS estimators are consistent.
goes to infinity, which implies that the OLS estimators are consistent.